경사하강법 (Gradient Descent)
이제 우리는 가정(모델) 함수를 가지고 있으며, 이것이 얼마나 데이터에 들어맞는지 측정할 방법도 있습니다. 이제 우리는 가정 함수의 파라메터를 추정해야 합니다. 경사하강법은 여기에 사용됩니다.
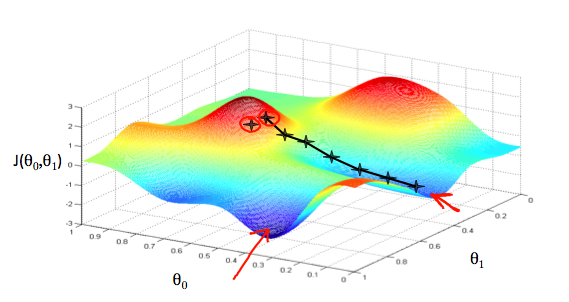
우리가 가정 함수를 와 에 기반한 그래프를 그린다고 해보겠습니다 (실제로 우리는 파라메터 추정의 함수로서 비용 함수를 그래프로 나타냅니다.) . 우리는 x 와 y 자체가 아닌, 우리 가정합수의 파라메터의 범위와 특정 파라메터를 선택했을 때의 비용 결과를 그래프로 나타냅니다.
를 x 축에 놓고 을 y 축에 놓고, 비용함수를 z 축에 놓았습니다. 그래프 상의 값은 특정 theta 파라메터로 우리의 가정을 사용했을 때, 비용함수의 결과 입니다.
우리는 우리의 비용함수가 우리 그래프의 구덩이의 바닥지점에 있을 때 성공한다는 것을 알게 될 것 입니다. 즉 해당값이 그래프의 최소값일 때 입니다. 빨간 화살표가 그래프의 극소점들을 가리킵니다.
이제부터 할 일은 비용함수의 미분 (함수의 접선)을 취하는 것입니다. 이 접선의 경사에서 우리는 다음번에 어느방향으로 진행할 것인지를 알 수 있습니다. 가파른 하강 방향으로 비용 함수를 단계적으로 내려갑니다. 각 단계의 크기는 학습 속도라고하는 매개 변수 α 로 정의합니다.
예를 들어, 위 그래프의 ‘별’ 표시는 우리가 α 파라메터로 결정한 (반복)간격입니다. 좀 더 작은 α 는 이것보다 촘촘하게 큰 것은 좀더 큰 간격으로 결과를 줄 것입니다. 각 간격사이의 방향은 의 편미분으로 결정합니다. 어느 지점에서 시작하는지에 따라서 결과는 다른 지점에서 완료됩니다. 상기 이미지에서는 두개의 다른 지점에서 시작하여, 각각 다른 지점에서 종료되는 것을 볼 수 있습니다.
경사하강 알고리즘은 이러한 진행을 수렴할 때까지 반복하는 것입니다.
여기서 j=0,1 은 특징(입력값)의 인덱스번호를 나타냅니다
각각의 반복 j 에서, 주의할 것은 파라메터 들을 동시에 갱신해야 합니다. 만약 특정 파라메터를 다른 것을 계산하기 전에 갱신한다면 반복시 잘못된 구현결과를 얻게 됩니다.
'머신러닝' 카테고리의 다른 글
| 선형회귀를 위한 경사하강법 (Gradient Descent For Linear Regression) (0) | 2018.10.02 |
|---|---|
| 경사하강법의 직관적인 이해(Gradient Descent Intuition) (0) | 2018.09.17 |
| 비용함수 (Cost Function) (0) | 2018.09.10 |
| 모델 표현(Model Representation) (0) | 2018.09.07 |
| 비지도 학습(Unsupervised Learning) (0) | 2018.09.06 |
경사하강법 (Gradient Descent)
이제 우리는 가정(모델) 함수를 가지고 있으며, 이것이 얼마나 데이터에 들어맞는지 측정할 방법도 있습니다. 이제 우리는 가정 함수의 파라메터를 추정해야 합니다. 경사하강법은 여기에 사용됩니다.
우리가 가정 함수를 와 에 기반한 그래프를 그린다고 해보겠습니다 (실제로 우리는 파라메터 추정의 함수로서 비용 함수를 그래프로 나타냅니다.) . 우리는 x 와 y 자체가 아닌, 우리 가정합수의 파라메터의 범위와 특정 파라메터를 선택했을 때의 비용 결과를 그래프로 나타냅니다.
를 x 축에 놓고 을 y 축에 놓고, 비용함수를 z 축에 놓았습니다. 그래프 상의 값은 특정 theta 파라메터로 우리의 가정을 사용했을 때, 비용함수의 결과 입니다.
우리는 우리의 비용함수가 우리 그래프의 구덩이의 바닥지점에 있을 때 성공한다는 것을 알게 될 것 입니다. 즉 해당값이 그래프의 최소값일 때 입니다. 빨간 화살표가 그래프의 극소점들을 가리킵니다.
이제부터 할 일은 비용함수의 미분 (함수의 접선)을 취하는 것입니다. 이 접선의 경사에서 우리는 다음번에 어느방향으로 진행할 것인지를 알 수 있습니다. 가파른 하강 방향으로 비용 함수를 단계적으로 내려갑니다. 각 단계의 크기는 학습 속도라고하는 매개 변수 α 로 정의합니다.
예를 들어, 위 그래프의 ‘별’ 표시는 우리가 α 파라메터로 결정한 (반복)간격입니다. 좀 더 작은 α 는 이것보다 촘촘하게 큰 것은 좀더 큰 간격으로 결과를 줄 것입니다. 각 간격사이의 방향은 의 편미분으로 결정합니다. 어느 지점에서 시작하는지에 따라서 결과는 다른 지점에서 완료됩니다. 상기 이미지에서는 두개의 다른 지점에서 시작하여, 각각 다른 지점에서 종료되는 것을 볼 수 있습니다.
경사하강 알고리즘은 이러한 진행을 수렴할 때까지 반복하는 것입니다.
여기서 j=0,1 은 특징(입력값)의 인덱스번호를 나타냅니다
각각의 반복 j 에서, 주의할 것은 파라메터 들을 동시에 갱신해야 합니다. 만약 특정 파라메터를 다른 것을 계산하기 전에 갱신한다면 반복시 잘못된 구현결과를 얻게 됩니다.
'머신러닝' 카테고리의 다른 글
| 선형회귀를 위한 경사하강법 (Gradient Descent For Linear Regression) (0) | 2018.10.02 |
|---|---|
| 경사하강법의 직관적인 이해(Gradient Descent Intuition) (0) | 2018.09.17 |
| 비용함수 (Cost Function) (0) | 2018.09.10 |
| 모델 표현(Model Representation) (0) | 2018.09.07 |
| 비지도 학습(Unsupervised Learning) (0) | 2018.09.06 |