개요
기하학적 데이터 처리는 이진 검색 트리(binary search tree)의 응용분야 중 하나입니다.
예를 들어 평면에 사각형이 놓여있고 점이 여기저기 분포해 있을 때, 어떠한 점이 사각형 내부에 있는지 또는 얼마나 많은 점이 사각형 내부에 포함되는지 알고 싶을 수 있습니다. 또는 점이 아닌 사각형이 여러 개 있는 경우 어떤 사각형이 서로 겹치는지 알고 싶을 수 있습니다.
우리는 이진검색트리를 이들 문제를 해결하는 데 사용할 수 있습니다. 그 경우 일반적으로 사용하는 문자열과 숫자가 아닌 기하학적 객체(점의 위치 등)를 키로 사용합니다.

1차원 범위검색 (1d Range Search)
정렬된 심볼테이블(Ordered Symbol Table)을 조금 확장하면 1차원 범위 검색과 범위 개수를 셀 수 있습니다.
키를 선분상의 점으로 생각하면 특정 위치 사이에 위치한 점들 또는 점의 개수를 구하는 것은 특정 키 사이의 키들과 키의 개수를 구하는 것과 동일합니다.

이진 검색 트리를 이용하면 rank를 이용하여 이 문제를 해결할 수 있습니다. 만약 E키와 S키 사이에 존재하는 키를 찾고자 하는 경우 해당 키의 rank를 구하여 이 차를 사용하면 됩니다.

참고 이진 검색 트리(BST, Binary Search Tree)에서 Rank란, 해당 키보다 작은 다른 키의 개수를 의미합니다. 위 그림에서
E키 보다 작은 키는A,C두 개 이므로 rank 가 2입니다.
F와 T사이에 존재하는 모든 키를 구하는 예시를 살펴보겠습니다. 루트 S에서 시작합니다. S는 F와 T사이에 존재하므로 범위 검색 결과에 추가합니다. 좌측으로 이동하면 E는 F보다 작으므로 범위검색 결과에는 추가하지 않고 오른쪽 트리만 검색합니다. R은 범위 내에 존재하므로 범위검색 결과에 추가한 후, 좌/우측 트리를 검색합니다. 이 과정을 반복합니다.
루트의 좌측 트리의 검색을 마쳤으므로 다시 루트로 돌아가 오른쪽 검색을 시작하면 X는 T보다 큰 값이므로 X의 왼쪽 트리만 검색합니다.

선분 교차 (Line Segment Intersection)
또 다른 기하학적 응용분야인 선분의 교차 여부를 구하는 문제를 살펴보겠습니다.
여러 선분이 수평과 수직으로 배치되어 있을 때, 각 선분이 서로 교차하는지 확인하고자 합니다. 각 선분 별로 다른 선분들과 겹치는지 확인하는 방법은 많은 수의 데이터를 처리할 수 없습니다. 문제의 간소화를 위하여 x와 y 좌표가 동일한 중복된 선분은 존재하지 않는다고 가정합니다.
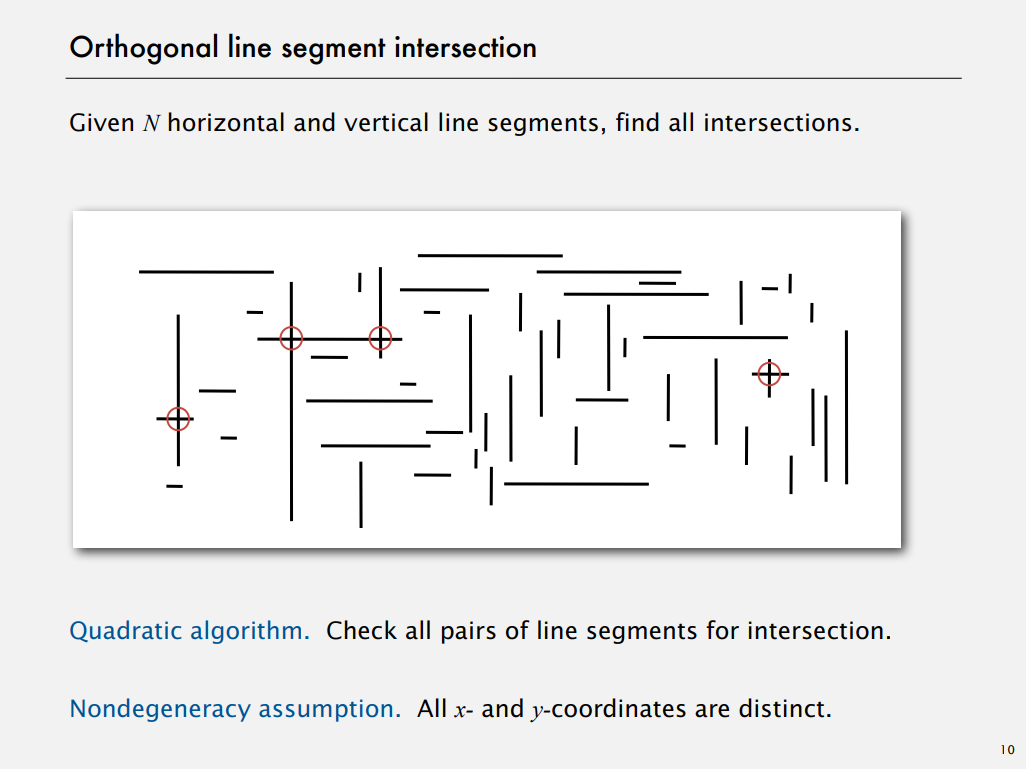
스윕 라인 알고리즘 (sweep-line algorithm)을 이용해 이 문제를 풀어보겠습니다.
왼쪽에서 오른쪽으로 이동하는 수직의 가상의 선분이 있습니다. 이것이 주어진 선분을 만날 때마다 아래 나열된 계산을 수행합니다.
- 수평선을 만나는 경우 y 좌표를 이진 검색 트리(BST, Binary Search Tree)에 삽입합니다.
- 수평선이 끝나는 경우 y 좌표를 이진 검색 트리에서 제거합니다.
- 수직선을 만나는 경우 해당 수직선의 시작점과 종료점을 키로 범위 검색을 수행합니다.

구현은 주어진 선분의 x 좌표를 우선순위 큐 (Priority Queue)에 넣고 이를 제거하면서 이벤트를 발생시킵니다. 해당 이벤트마다 앞서 언급하였던 계산을 수행하도록 합니다.
Kd-Trees
Kd 트리는 이진 검색 트리의 확장 버전으로 공간에 있는 일련의 점들을 효율적으로 처리할 수 있습니다.
앞서 제시하였던 문제 중, 평면상에 있는 여러 점 중 특정 사각형 영역 내부에 있는 점과 그 개수를 구하는 문제를 풀어보겠습니다. (이 문제는 데이터베이스에서 2가지 조건을 동시에 만족하는 데이터를 구하는 것과 동일합니다.)
앞서 문제와 같이 각 점과 평면을 개별적으로 비교를 한다면 많은 입력을 처리할 수 없을 것입니다. 검색 대상이 되는 후보를 줄여야 합니다.

검색 대상을 줄이기 위하여 평면을 M x M 격자로 나누고 각 격자에 속하는 점들을 목록으로 만듭니다. 범위 검색은 격자 중 직사각형과 겹쳐지는 격자에 대해서 수행합니다.

격자의 크기 M을 어떻게 선택하는가에 따라서 공간과 시간 간에 트레이드오프가 발생합니다
점의 정보를 저장할 공간은 M^2 + N
하나의 격자를 검사하는데 걸리는 시간은 1 + N/M^2의 관계가 됩니다.
너무 크지도 작지도 않은 M의 값은 대개의 경우 root(N) x root(N)의 격자로 구성하면 어느 정도 맞아떨어집니다.

격자를 통한 접근법은 골고루 분산되어 있는 점에 대해서 구현하기 쉬운 해법이지만 일반적으로 Clusting이라는 지리적인 데이터에서 나타나는 현상으로 인하여 격자를 통한 접근법만으로 해결하기는 어렵습니다.

공간을 조금 더 적절히 나누는 방법은 공간분할 트리(Space-partitioning trees)를 사용하는 것입니다. 트리의 노드에서 공간을 절반씩 나눈다면 2-d트리가, 4등분 한다면 4-d 트리가 될 것입니다.

자료구조는 다음과 같이 한 점을 기준으로 가상의 수직선과 수평선을 번갈아가며 그어가며 공간을 분할해 가는 방식으로 2-d 트리를 생성합니다.

2d 트리의 생성
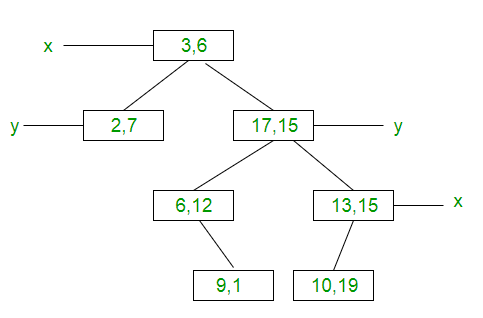
예를 들어 (3, 6), (17, 15), (13, 15), (6, 12), (9, 1), (2, 7), (10, 19)의 점이 주어졌을 때 이를 이용해 2d 트리를 구성해보겠습니다.
- (3, 6) 삽입 : 트리가 비어 있으므로 루트 노드에 삽입합니다.
: Since tree is empty, make it the root node. - (17, 15) 삽입 : 루트 노드의 x 좌표(3)와 크기를 비교합니다. 17은 3보다 크기 때문에 루트노드의 오른쪽에 삽입합니다.
- (13, 15) 삽입 : 루트 노드와 x 좌표(3)와 크기를 비교합니다. 13은 3보다 크므로 오른쪽에 삽입합니다. 해당 노드에는 (17,15)가 있습니다. 이번에는 (17, 15)의 y 좌표 (15)와 비교합니다. 서로 같은 값이기 때문에 (17, 15)의 오른쪽에 삽입합니다.
- (6, 12) 삽입 : 루트 노드의 x 좌표(3)보다 크기 때문에 오른쪽에 삽입합니다. 해당 노드에는 이미 (17, 15)가 있습니다. 이번에는 (17, 15)의 y좌표(15)와 비교합니다. 12는 15보다 작으므로 (17, 15)의 왼쪽에 삽입합니다.
나머지 (9,1), (2,7), (10, 19) 도 동일한 방식으로 삽입합니다. 완성된 트리는 다음 그림과 같습니다.
이번에는 그림의 녹색 사각형 내부에 있는 모든 점을 찾아야 한다고 해보겠습니다. 루트에서 시작합니다.
- 점 1은 사각형의 오른쪽에 위치하므로 트리의 좌측을 검색합니다.
- 점 3은 사각형을 가로지르므로 양쪽 트리를 모두 검색합니다.
- 점 4는 사각형의 오른쪽에 있으므로 왼쪽 트리만 검색합니다.
- 점 5는 사각형에 포함되고, 사각형을 가로지르므로 양쪽 트리를 모두 검색합니다.
- 다시 점 3으로 돌아가 오른쪽 트리를 확인합니다.
- 점 6은 오른쪽에 있으므로 왼쪽 트리만 검색합니다.

최근접 이웃 탐색 (Nearest neighbor search)
출처 : https://en.wikipedia.org/wiki/K-d_tree#Nearest_neighbour_search
최근접 이웃 탐색이란 요청받은 점에서 가장 가까운 점을 찾는 것이 목적입니다.
k-d 트리를 이용한 최근접 이웃 탐색은 다음 절차에 따라 진행됩니다.
- 루트 노드에서 시작합니다. 알고리즘은 트리를 재귀적으로 탐색합니다.
- 어떤 노드에 도착하면 현재 알려진 최고 근접한 값과 비교하여 해당 노드가 더 근접하다면 이 값으로 갱신합니다.
- 알고리즘은 각 노드에서 다음 과정을 수행하며 트리의 탐색을 진행합니다.
- 만약 현재 평가 중인 노드가 현재까지 알려진 근접 값보다 더 가까운 경우 현재 노드를 최근접 값으로 갱신합니다.
- 다른 측에 현재 노드보다 더 가까운 점이 존재할 수 있는지 확인합니다. 개념적으로 현재 알려진 가장 가까운 점과의 거리를 반경으로 하는 동심원과 노드에서 그은 분할선이 겹치는지 확인합니다.
- 분할선이 겹치는 경우는 해당 평면에 더욱 가까운 점이 있을 가능성이 있으므로 해당 영역도 탐색합니다.
- 겹치는 부분이 없다면 해당 영역의 탐색을 중단하고 상위로 올라갑니다.
- 루트 노드에 대한 탐색이 완료되면 최근접 이웃점을 찾은 것입니다.
참고
'알고리즘 트레이닝 > 자료구조' 카테고리의 다른 글
| 이중연결리스트(Doubly Linked Lists) - C++ (0) | 2020.05.14 |
|---|---|
| 단일연결리스트(Singly Linked Lists) - C++ (0) | 2020.05.01 |
| 덱(Deque, double-ended queue) (0) | 2018.12.16 |
| 원형큐 (0) | 2018.10.24 |
| 자료구조와 추상자료형 (0) | 2018.07.10 |
