앞선 포스트에서 정리하였던 것과 같이 경사하강 알고리즘은 비용함수를 미분하여 경사를 획득하고 이 경사값을 따라 진행해가며 그 값이 수렴할 때까지 반복하는 것입니다.이를 수식으로 표현하면 아래와 같이 요약됩니다.θj:=θj−α∂∂θjJ(θ0,θ1) \theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) θj:=θj−α∂θj∂J(θ0,θ1)선형회귀의 경우에 대해서 구체적으로 이를 적용해 보도록 하겠습니다.이를 위하여 비용함수와 가설함수를 선형회귀의 비용함수와 가설함수로 교체하도록 합니다.우선 선형회귀의 비용함수는 다음과 같습니다.J(θ0,θ1)=12m∑i=1m(y^i−yi)2=12m∑i=1m(hθ(..
경사하강법

경사하강법의 동작에 대해서 살펴보기 위하여 문제를 간단히 해보도록 합니다.하나의 입력 파라메터 θ1\theta_1θ1 만을 고려한 비용함수를 이용하여 비용하강 알고리즘에 대하여 살펴보겠습니다.하나의 입력 파라메터만을 사용할 경우, 아래의 결과 값이 수렴할 때까지 반복하게 됩니다. θ1:=θ1−αddθ1J(θ1) \theta_1:=\theta_1-\alpha \frac{d}{d\theta_1} J(\theta_1) θ1:=θ1−αdθ1dJ(θ1)위 과정은 비용함수(J(θ)J(\theta)J(θ))의 경사값의 부호(+, -)와 관계 없이 비용함수의 최소값 수렴하게 됩니다. 그 과정은 아래의 그림에 표현되어 있습니다.경사값이 양수일 경우, 새로 갱신되는 θ\thetaθ 값은 이전의 θ\thetaθ..
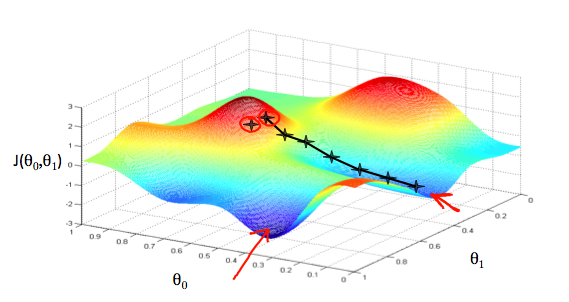
경사하강법 (Gradient Descent) 이제 우리는 가정(모델) 함수를 가지고 있으며, 이것이 얼마나 데이터에 들어맞는지 측정할 방법도 있습니다. 이제 우리는 가정 함수의 파라메터를 추정해야 합니다. 경사하강법은 여기에 사용됩니다.우리가 가정 함수를 θ0\theta_0θ0 와 θ1\theta_1θ1 에 기반한 그래프를 그린다고 해보겠습니다 (실제로 우리는 파라메터 추정의 함수로서 비용 함수를 그래프로 나타냅니다.) . 우리는 x 와 y 자체가 아닌, 우리 가정합수의 파라메터의 범위와 특정 파라메터를 선택했을 때의 비용 결과를 그래프로 나타냅니다.θ0\theta_0θ0 를 x 축에 놓고 θ1\theta_1θ1 을 y 축에 놓고, 비용함수를 z 축에 놓았습니다. 그래프 상의 값은 특정 thet..